红黑树
二叉树、平衡树、AVL 树和红黑树
二叉树是一类特殊的树形结构,其他类似的还有三叉树、B 树、B+树等,二叉树的特征是 1 对 2,即每个节点都有 2 个子节点(这里认为空节点也算子节点)。
这么定义主要是为了避免将二叉树的实现局限于指针,实际上我们也可以使用数组来实现二叉树,也就是二叉堆。
二叉树所有操作的时间复杂度为O(logN),但是它存在的主要问题是不稳定,比如数据是从小到大依次插入的情况下,最终结果是得到一条斜线,这时二叉树会退化为链表。
平衡树的特点是在每次写入操作后会进行一次重平衡,让树的高度保持在O(logN)。
AVL 树是平衡树的一种,它严格保证树的高度为O(logN),每次都会根据高度重平衡,其缺点是过于严格,会导致旋转操作占用比较多的时间。
红黑树作为 AVL 树的一种替代,通过红黑规则控制树的旋转,能以较少次旋转作为代价得到较为平衡的树。
AVL 树严格保证树的高度在
[logN, logN + 1],红黑树理论上极端情况可以出现高度达到 2*logN,但是现实中很难遇到。
红黑树的起源 - 23树
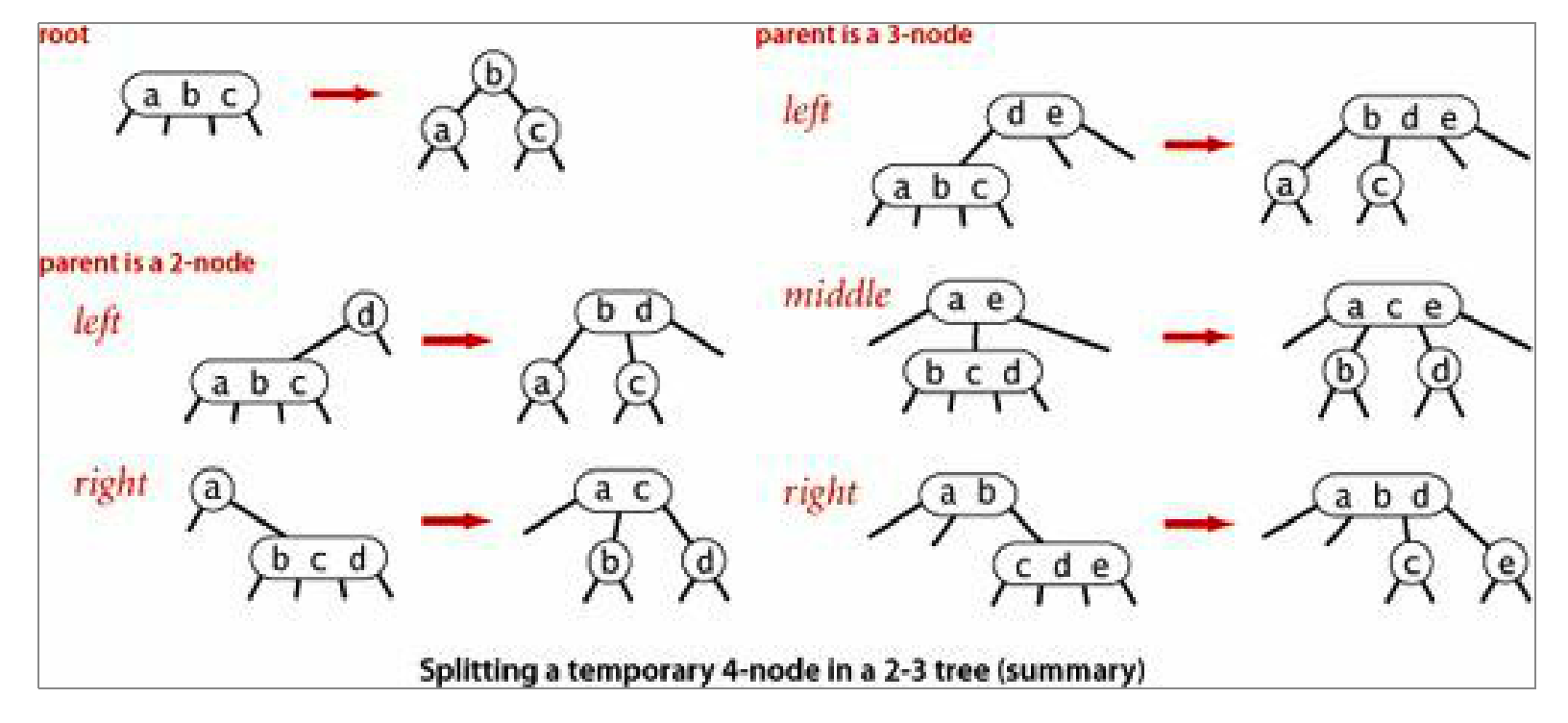
23树并不是指3叉树,23树是一种平衡树,不过它维持平衡的方式并不是旋转,而是分裂,如上图所示:
- 一个节点有至多3个元素,当达到3个元素后会发生分裂;
- 分裂后中间元素上移,与父节点合并。
23树可以证明高度在log3(N)=(lgN)/(lg3)(如果都是3-nodes即2元素节点)到lgN(如果都是2-nodes即1元素节点),从而保证查询时顶多查lgN个节点。
23树的缺点是实现的额外开销过大,比如要变更节点类型、比较是否相等时要比较节点中的所有元素值等,有时候23树的性能甚至不如普通的BST,因此Sedgewick之后便提出了红黑树。
红黑树的定义
红黑树是从23树演化而来的,它将原来2-3树中的3-nodes表示为使用红线连接的两个节点,因为每个节点只有一条线连上它,因此为了简单起见把颜色字段保存到节点里。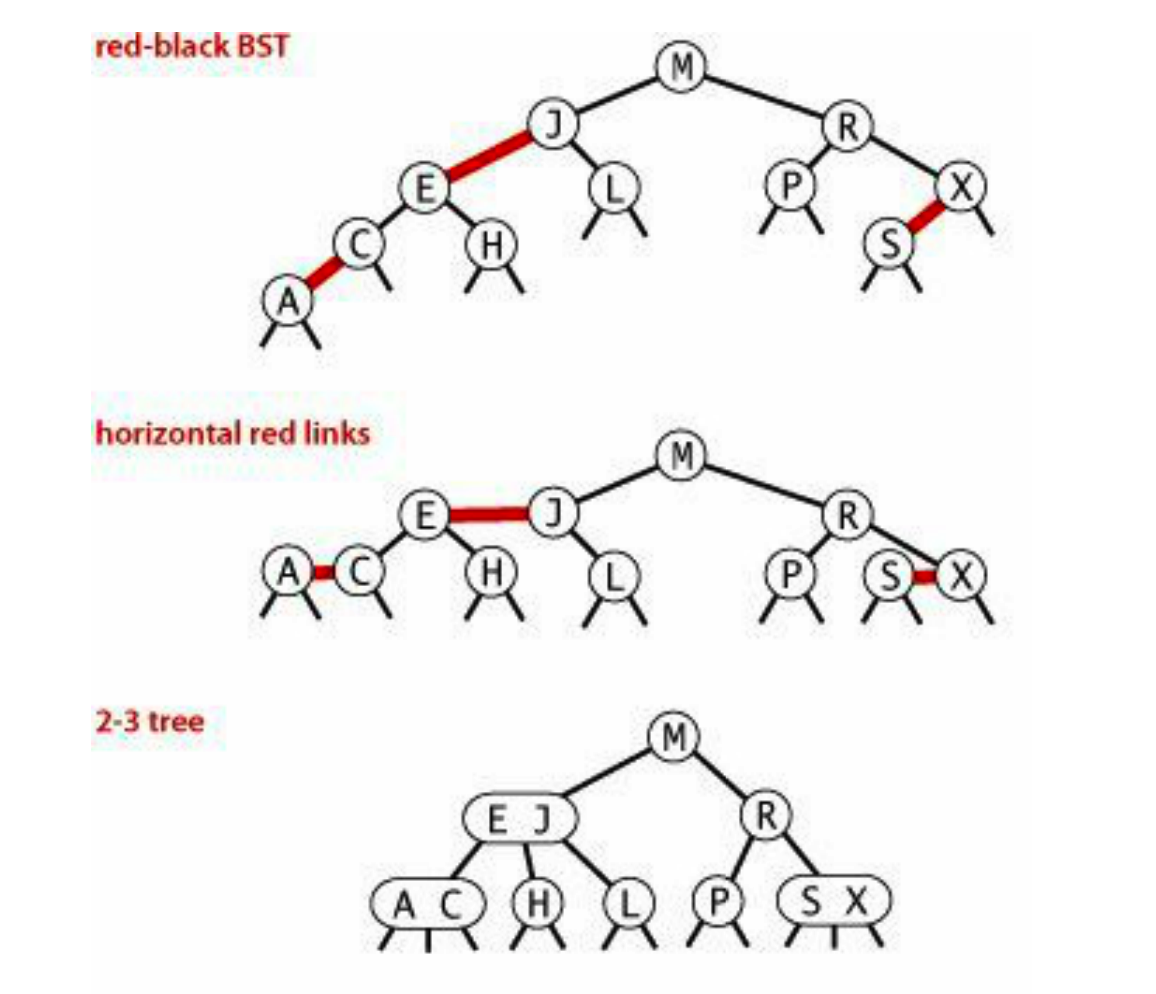
红黑树的定义:
- Red links lean left. - 红色节点必须在左边
- No node has two red links connected to it. - 3个红色节点不能连一起
- The tree has perfect black balance: every path from the root to a null link has the same number of black links. - 红黑树是完美黑平衡的,从root沿任意路径到达叶节点的黑节点数量都是一样的。
以上3个定义其实和2-3树的定义是一一对应的:
- 和左红节点连一块可以看作2-3树中的一个3-node;
- 2-3树中一个节点中塞满3个元素后就会分裂;
- 把红黑树中节点和其左红子节点合并后,最终的树其实和2-3树等价。
红黑树的红黑规则:
- 任何一个节点都有颜色,黑色或者红色;
- 根节点是黑色的;
- 空节点(有些实现中叶节点是哨兵节点nil)被认为是黑色的。
- 父子节点之间不能出现两个连续的红节点(如果父节点是红色,则它的两个儿子都是黑色);
- 任何一个节点向下遍历到其子孙的叶子节点,所经过的黑节点个数必须相等;
红黑树操作 - 查询
红黑树的查询就是普通的二叉树查询。
红黑树操作 - 旋转
左旋操作将右子节点旋转到父节点位置,并改变二者的颜色。
右旋同理: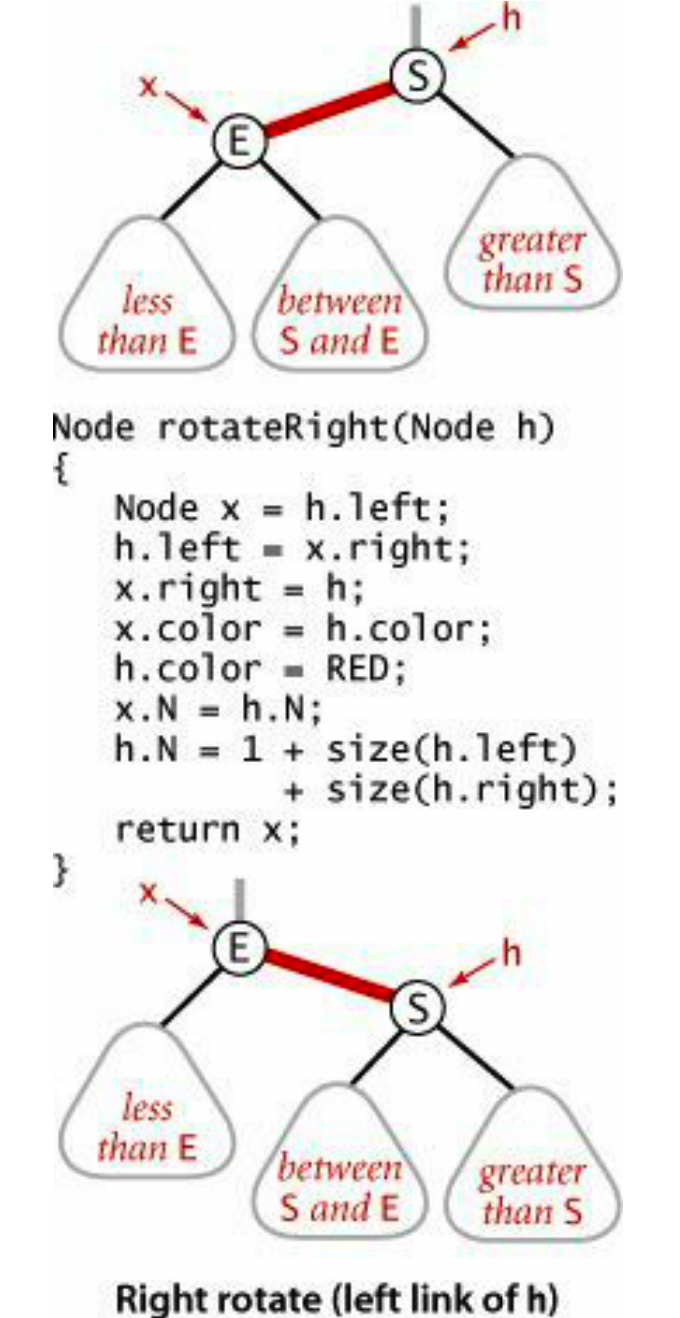
红黑树操作 - 插入
红黑树的插入操作和 BST 差不多,只不过插入后可能会破坏上面红黑树的定义,因此需要做一些旋转和颜色修改操作来恢复。
很多地方描述红黑树的方式并不一致,这里还是以《算法》中的实现为主。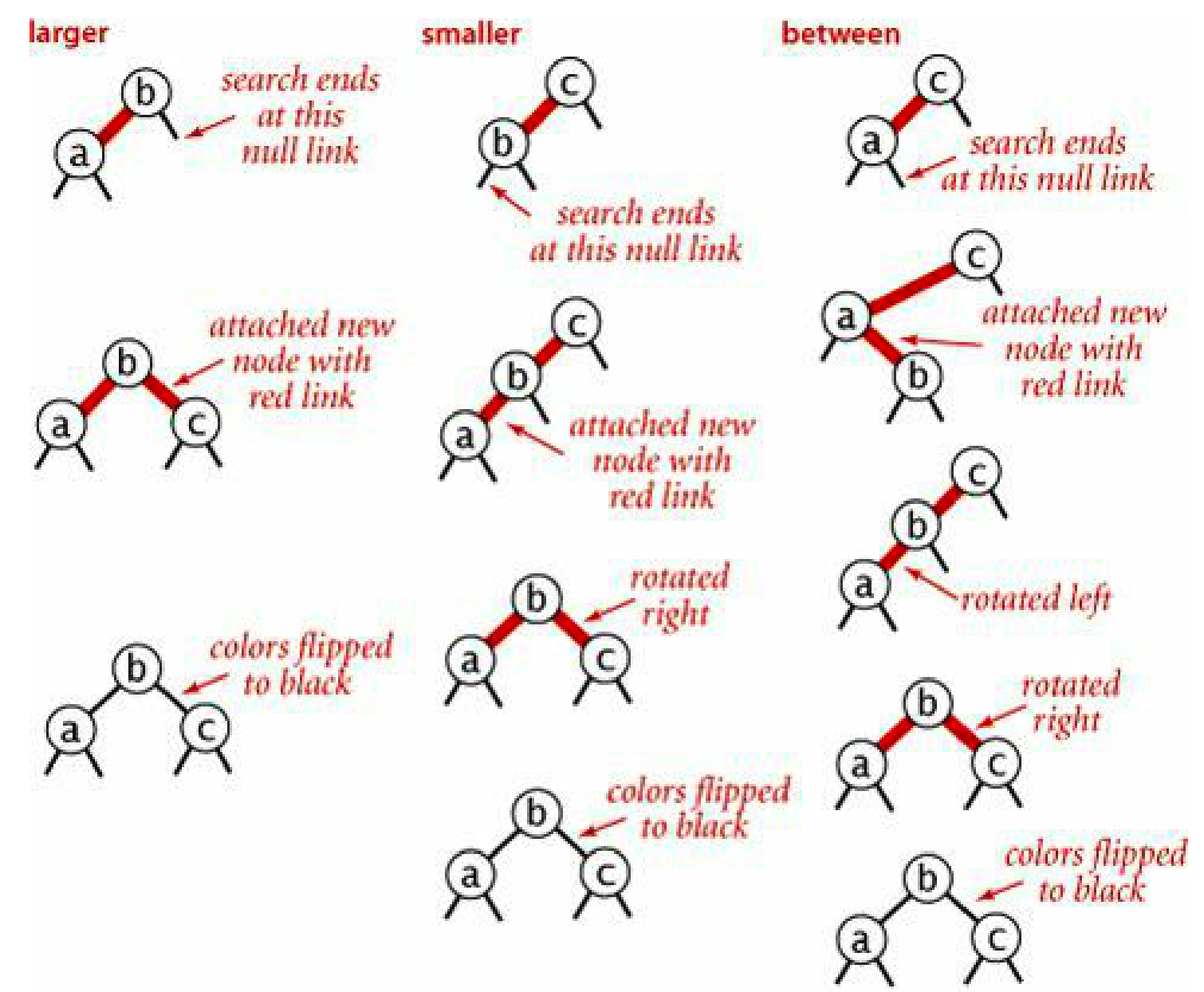
- 可以看到上面3种情况最终都转换成了一个三角形的形状,然后进行了颜色的翻转,实际上相当于2-3树中一个3元素节点分裂成了3个。
下图是一个插入节点到红黑树中的例子,其中被红线连接的子节点是红色的节点: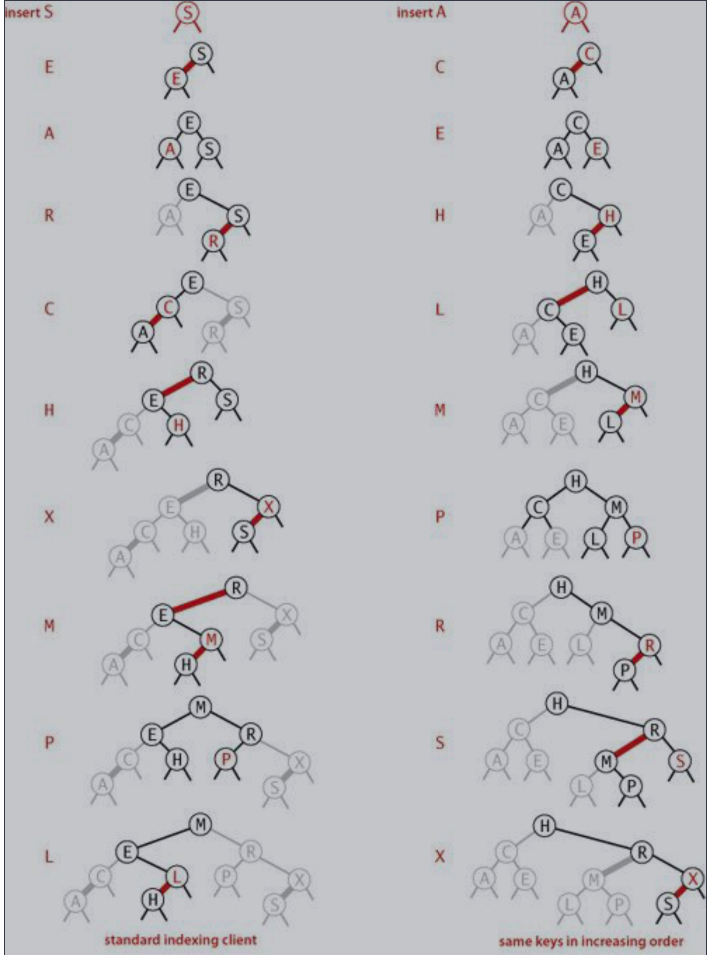
红黑树操作 - 删除
参考
- 《Algorithms》 - Robert_Sedgewick
红黑树原来是从23树演化而来,之前以为是凭空编出来的。 - 《Algorithms》中的红黑树实现